확률 및 통계(6)
한양대학교 이상화 교수님의 확률 및 통계 강의를 수강하고 정리한 내용입니다

- Nomal Distribution는 가우시안 분포라고도 불리고, RV가 Continuous RV일 경우에 사용됩니다.
- 정규분포의 pdf식은 슬라이드에서의 f(x)와 같습니다. 정규분포의 pdf는 분산의 크기에 따라 완만하거나 가파른 형태를 띕니다.
- single-mode(볼록한 부분), Symetric(대칭성), Bell-shaped의 특징들을 갖고 있습니다.
CDF
- 정규분포의 cdf는 pdf의 적분을 통해 나타낼 수 있습니다.
- 전체 구간에 대한 값은 1을 갖습니다.
- 특정 구간에 대한 CDF는 표준정규분포를 이용하여 계산할 수 있습니다.

이전 강의에서 배웠던 Binomial distribution은 Bernoulli trail을 기반으로 하기에 특정 구간에서의 확률을 계산할 경우 가능한 조합을 일일이 계산하기가 어렵기에 Nomal Distribution으로 바꿔서 쉽게 구할 수 있습니다. 이항분포를 정규분포로 바꿔주면 N(np, np(1-p))형태가 됩니다. 이를 특정 구간 a, b에 대해서 정규화를 진행하고, Look-up table을 참고하여 쉽게 계산이 가능합니다.

Error function과 Complementry Error function은 또 다른 Look-up table입니다. Error function과 Complementry Error function을 통해 특정 구간에서의 확률을 쉽게 구할 수 있습니다.

Pascal Distribution은 Bernoulli trail을 k번 성공할 때 까지 시도한 횟수에 대한 확률 분포입니다. P(x)는 마지막 n번째 시행에서 k번째 성공을 해야 하기에 n-1번까지의 시행동안 k-1번의 성공을 해야하기에 조합과 이항분포의 식을 이용하여 정의할 수 있습니다.

이전 강의까지는 일변수에 대한 Sample space에 대해서 배워왔습니다. 앞으로 배울 Chapter 5부터는 Multiple RV에 대한 확률 분포에 대하여 배우게 됩니다. 우선 변수가 2개인 경우에는 각각의 변수에 mapping되는 2개의 Sample space가 존재합니다. 2개의 Sample space를 Joint하는 경우에는 순서쌍 형태로 표현하게 되어 왼쪽 하단과 같은 형태가 되고, mapping되는 Sample space도 순서쌍의 형태로 표현합니다.


2개의 확률변수에 대한 CDF함수는 Fxy(x,y)형태로 나타내고, Multiple RVs CDF은 1) ~ 6)의 특징을 갖고 있습니다.

2개의 Discrete RV경우 P(X=x, Y=y) = Pxy(x,y) 형태로 나타낼 수 있고, 1)~5)의 특징을 갖고 있습니다. 마지막 5) 특징은 각 사건이 독립인지 종속인지 판단하는데 사용되는 특성입니다.
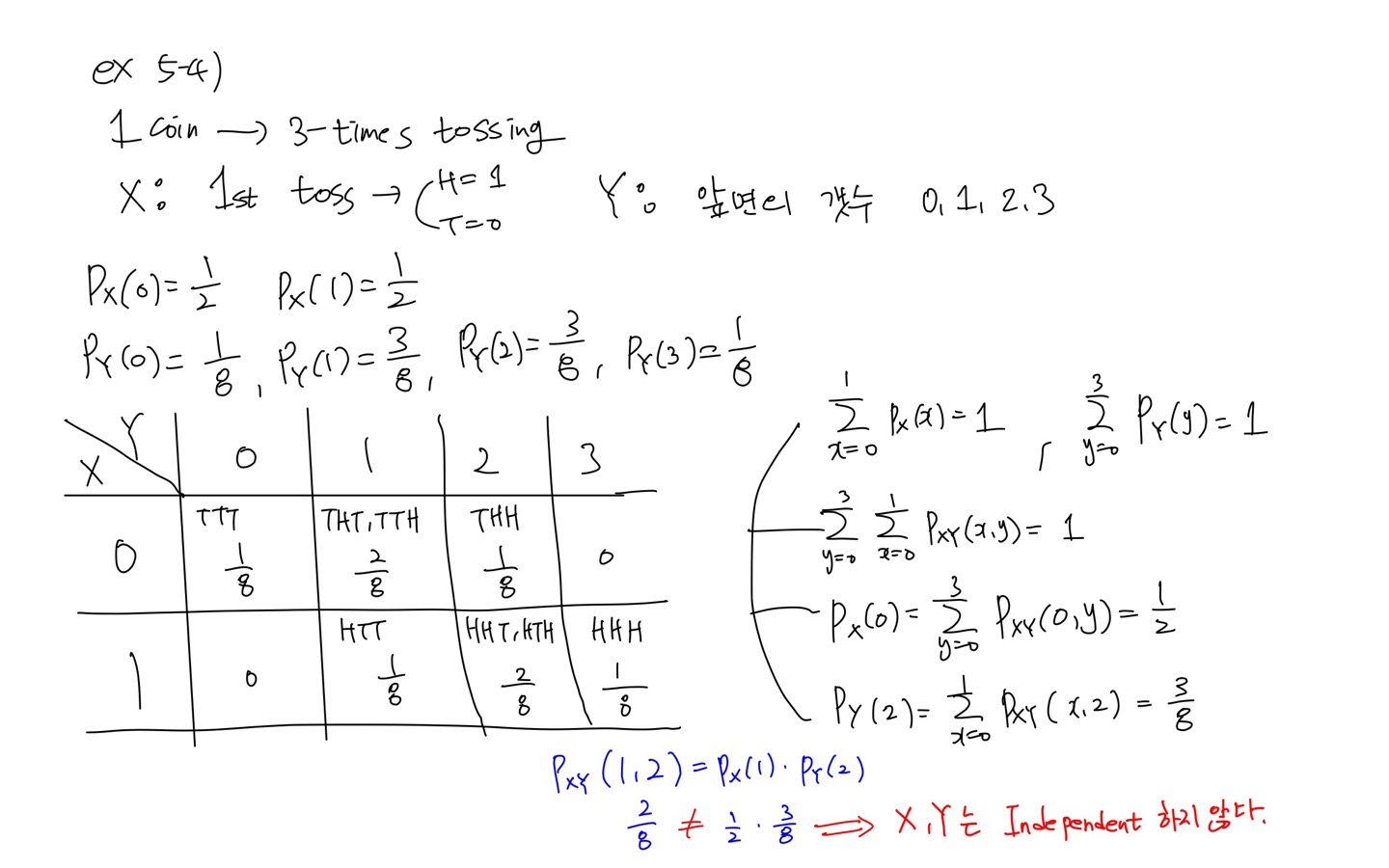
1개의 동전을 3번 던질 때, 첫번째 시도에서 앞, 뒷면이 나올 확률 변수 X와 최종적으로 나온 앞면의 갯수를 확률 변수 Y로 설정하여 두개의 변수가 독립인지 아닌지 판단해보겠습니다. Pxy(1,2)는 첫번째 시도에서 동전의 뒷면이 나오고, 총 앞면의 갯수가 2개 나올 확률을 의미합니다. 동전을 3번 던져서 첫번째 시도에서 동전의 뒷면이 나오고, 총 앞면의 갯수가 2개 나오는 경우의 수는 HHT, HTH로 2개가 있으니 Pxy(1,2) = 2/8입니다. 이번에는 X와 Y를 따로두고 생각해보면, 첫번째 시도에서 동전의 뒷면이 나올 확률은 1/2이고, 동전의 앞면의 갯수가 총 2개 나올 확률은 3/8이므로, 둘의 곱이 Pxy(1,2)와 같지 않기 때문에 두 확률 변수 X, Y는 Independent하지 않다는 결론이 나오게 됩니다.

이번에는 2개의 Continuous한 확률 변수에 대한 확률 분포에 대해서 생각해보겠습니다. cdf는 항상 그래왔듯이 pdf를 적분하여 구할 수 있는데, 확률변수가 2개 있기 때문에 2개의 확률변수에 대해 각각 편미분을 시행해줘야 합니다. 또한 Continuous RVs의 확률분포는 1)~5)같은 특징을 갖고 있습니다.