한양대학교 이상화 교수님의 확률 및 통계 강의를 수강하고 정리한 내용입니다

Bernoulli Distribution은 outcome이 2개인 경우 real number로 mapping하는 RV의 분포를 의미합니다. Success, fail 처럼 2개의 outcome에 대한 확률 분포가 예시이고, 평균과 분산은 다음과 같습니다.

Binomial Distribution은 2개의 outcome만 나오는 Bernoulli trail을 N번 시행했을 때, 성공 횟수를 RV로 정의한 확률 분포입니다. RV는 1~n으로 discrete한 값이고, 이항정리를 이용하여 평균과 분산을 계산할 수 있습니다.

Geometric Distribution은 Bernoulli trial에서 첫번째로 성공하는 시행 횟수를 RV로 정의한 확률 분포를 말합니다. x는 discrete하며, Forgetfulness라는 성질을 갖고 있습니다. Forgetfulness는 이전까지 시행했던 것이 앞으로의 시행 확률에 영향을 주지 않는 것을 말합니다. 간단하게 예시를 들면 동전을 10번 던지는 동안 앞면이 나오지 않았더라도, 앞으로 동전의 앞면이 나올 확률은 1/2로 이전 시행의 확률에 영향을 받지 않는 것을 생각하면 됩니다.

- Poisson Distribution은 주어진 시간동안 Bernoulli event가 몇번 발생했는지에 대한 확률 분포를 말합니다. 예를 들면 주어진 1시간 동안 도착하는 패킷의 수와 같은 것을 생각해 볼 수 있습니다.
- Exponential Distribution은 특정 시점까지 System이 생존할 확률에 대한 확률 분포를 말합니다. Exponential Distribution도 Forgetfulness 성질을 갖고 있는데, 주어진 t시점까지 생존에 성공했을 때, 추가로 s라는 시간동안 생존할 확률은 이전 t시점까지의 생존 확률이 영향을 주지 않습니다.

Erlang Distribution은 Exponential Distribution의 일반화된 형태를 말합니다. Erlang Distribution의 RV는 특정 갯수 K+1개가 연속적으로 발생하는 event들의 시간 구간을 의미합니다. Erlang-K Distribution은 K개의 time interval을 더한 확률분포를 말하는데, k=1을 대입하면 이전에 배운 Exponential Distribution의 식이 됩니다.
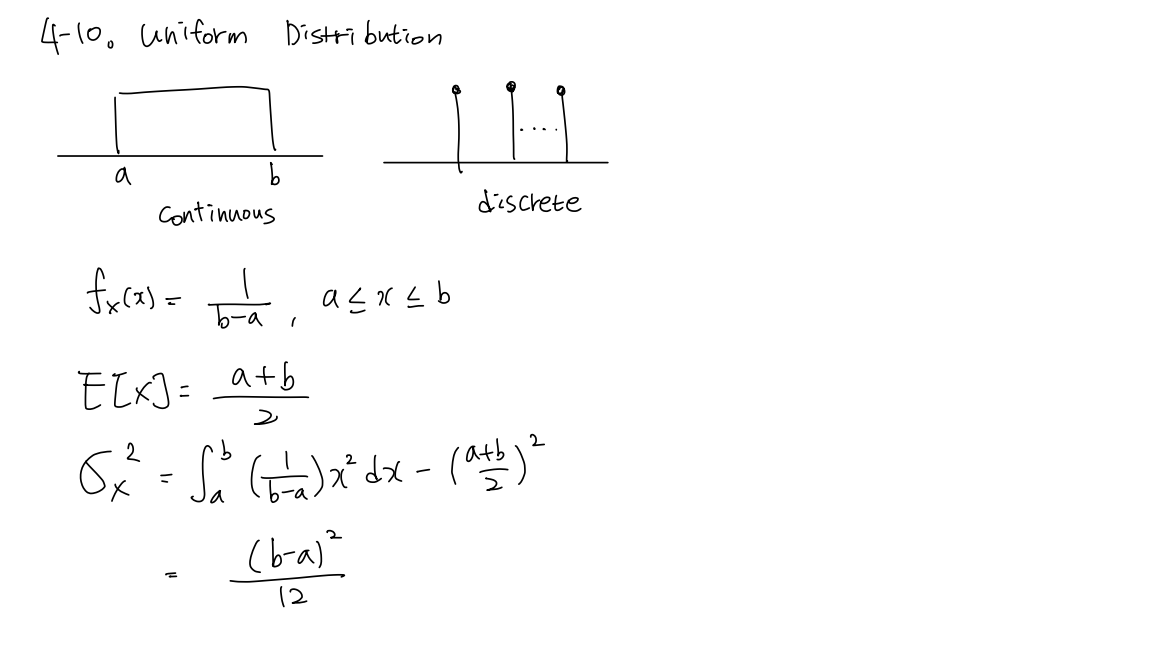
Uniform Distribution은 Continuous RV, discrete RV 모두 가능하고, 평균은 두 구간의 사이값으로 구할 수 있고, 분산은 pdf를 cdf로 바꾸는 적분과정을 통해 구할 수 있습니다.
'Mathematics > Probability and Statistics' 카테고리의 다른 글
| 확률 및 통계(7) (0) | 2024.04.23 |
|---|---|
| 확률 및 통계(6) (0) | 2024.04.22 |
| 확률 및 통계(4) (0) | 2024.04.20 |
| 확률 및 통계(3) (0) | 2024.04.20 |
| 확률 및 통계(2) (1) | 2024.04.19 |






댓글