확률 및 통계(7)

한양대학교 이상화 교수님의 확률 및 통계 강의를 수강하고 정리한 내용입니다

 

 

 

 

Conditional Distribution(조건부 확률)에 대해 알아보겠습니다. 조건부 확률은 RV가 Discrete한 경우와 Continuous한 경우로 나눠서 알아보겠습니다. 우선 Discrete한 경우는 이전에 예시로 들었던 1개의 동전을 3번 던지는 수행으로 보면, 우선 Joint 확률 표를 작성하고, 확률을 구할 수 있습니다

 

 

 

 

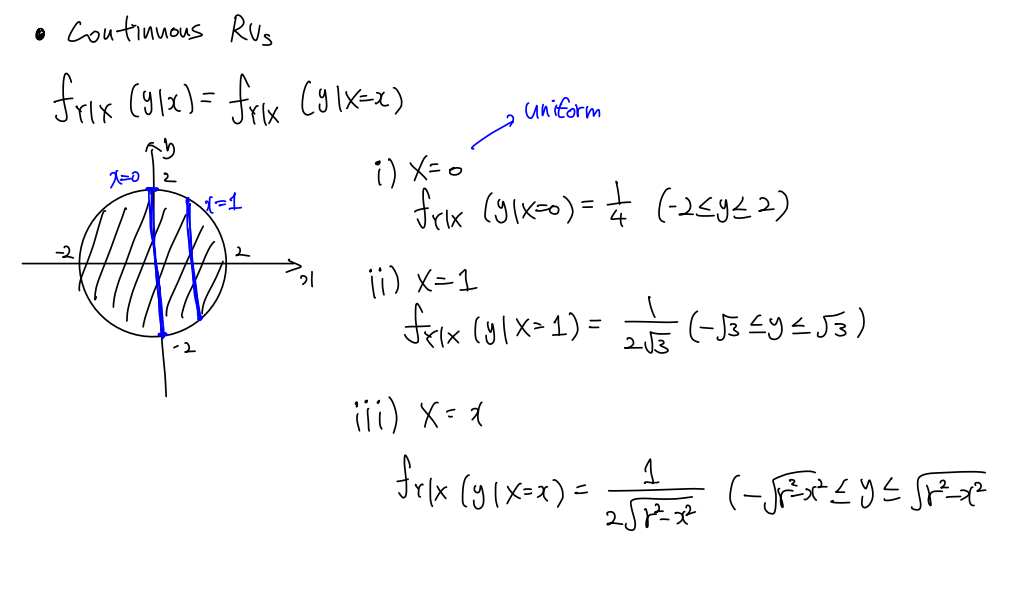
Continuous한 경우는 위처럼 원의 경우에 조건부 확률을 구하면 Uniform Distribution로 나오게 됩니다. 

 

 

 

 

위 슬라이드에서 정리한 것 처럼 극한의 개념을 이용하면 CDF의 미분을 통해 PDF를 계산할 수 있고, 최종적으로 좌측 하단에 나온 것처럼 조건부 확률 분포 PDF에 대한 식이 나오게 됩니다. 

 

 

 

 

Conditional Mean은 Multiple RVs 조건부확률의 평균값으로 Continuous한 경우에는 [-무한대 ~ + 무한대] 까지의 Yx PDF의 적분을 통해 구하면 됩니다.

 

 

 

 

공분산과 상관계수에 대해서 배우게 됩니다. 공분산과 상관계수는 2개의 서로 다른 Random variable의 경향이 서로 어떤지 파악하기 위해 사용됩니다. 공분산 Cov(X,Y)는 위의 슬라이드에서의 식처럼 표현할 수 있습니다. 만약 Cov(X,Y) = 0이라면 확률변수 X와 Y는 서로 상관성이 없다는 것을 의미합니다.

그렇다면 여기서 이런 질문을 해볼 수 있습니다. "만약 두 확률 변수 X와 Y가 independent하다면 Cov(X,Y) = 0 일까?"

정답은 "그렇다" 입니다. 그렇다면 그 역도 성립을 할까요? 그렇지는 않다고 합니다.

 

 

 

 

다음으로는 상관계수에 대해서 배웁니다. 상관계수란 위의 식에서 쓰여있듯 공분산을 2개의 확률변수 X와 Y 각각의 표준편차를 곱한값으로 나눠주는 것입니다. 상관계수는 -1~+1까지의 범위를 갖고 있는데, 상관계수가 1에 가까울수록 X와 Y가 서로 같은 방향성을 갖는 것을 의미하고, -1에 가까울수록 서로 다른 방향성을 갖는 것을 의미하고, 0에 가까울수록 서로 상관이 없다는 것을 의미합니다. 여기서 서로 같은 방향성을 갖는다는 것은 X가 증가하면 Y도 증가한다는 것을 의미합니다.